1962年提出了电磁流量计权重函数理论，较好地解释了电极所在平面上不同点的液体流速对传感器输出信号的贡献。在此后的电磁流量计研究过程中，研究者依据权重函数理论对电磁流量计技术进行了深入的研究，如SmythCC等人采用复变函数映射和Green定律求出圆管和矩形管下不同电极电磁流量计的权重函数和输出信号，O’Sullivan和Al-KhazrajitYA等人对多电极和大电极电磁流量计权重函数进行了相应的研究。
  现有研究资料表明，电磁流量计权重函数的研究前提是假设在满管状态下管内流速呈轴对称分布，而对用于非满管测量的电磁流量计权重函数还没有作较为完整的理论研究。本文采用有限元数值分析方法，对长弧形电极非满管电磁流量传感器的权重函数进行了研究，给出了不同液位下的权重函数分布图谱，从而为非满管电磁流量传感器结构的优化设计及标定提供了理论依据。

    1 权重函数有限元数值计算

    1.1 权重函数求解算法

    长筒式电磁流量计物理模型如图1所示。

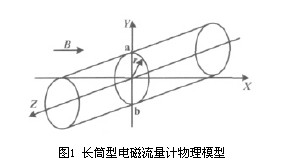
    由图1可知，被测流体沿流量计测量管的Z轴方向流动，电磁流量计励磁系统产生磁场。在流量计测量管内壁装有电极a和电极b，用于测量流体作切割磁力线产生的感应电势。

    ShercliffJA首先对普通长筒式电磁流量计进行了系统的分析，提出了权重函数理论。Bevir于1970年对权重函数作了进一步阐述，在相应的假设条件下，给出了电磁流量测量基本方程的积分形式，即：

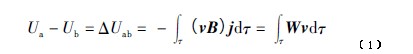
    式中：τ为所有流动的流体空间体积；（Ua－Ub）为电磁流量传感器测量电压；v为管内流体的流速；B为磁场强度；W为权重函数。

    W的计算式为：

    W=Bj  （2）

    式中：j为虚电流密度，它是Bevir引入的一个重要概念，其值由电磁流量传感器的电极结构形式和测量管内壁的电边界条件决定。

    j表示的物理意义是：如果假定流体为静止不动，同时有单位电流从流量计正电极流入被测流体并从负电极流出，由于这种电流实际不存在，故称为虚电流。虚电流密度j和磁场强度B可进一步用势函数来表示，即：

    j=-ÑG（3）

    B=-ÑF（4）

    W可表示为：

    式中：G和F为引入的标量势函数。

    由于在传感器测量管内只有被测流体，没有电源和磁源，则在非满管传感器被测流体截面内势函数满足Laplace方程，即：

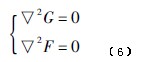
    权重函数由势函数G和F决定，故求解权重函数变成求解势函数G和F的边值问题。根据给定的边值条件，求解式（6）可得势函数G和F的分布，再根据G和F得到虚电流密度j和磁场B的分布，从而求得权重函数W。

    如果流速为轴向直线流（沿Z轴），则根据式（2）可得：

    式中：jX、jY和BX、BY分别为X轴方向和Y轴方向的虚电流密度和磁场强度分布。

    若电磁流量计测量管内磁场方向沿X轴方向，且沿Y轴方向的磁场BY=0，则权重函数可以表示为：

    同样地，如果磁场方向沿Y轴方向，且沿X轴方向的磁场BX=0，则权重函数可以表示为：

  
  因此，根据电磁流量计测量管内虚电流和磁场强度即可求得权重函数。

    1.2 权重函数有限元数值求解

    在一定的传感器结构下，测量管内的虚电流密度和磁场强度的分布可通过有限元数值分析方法求取，从而实现数值分析方法求取权重函数。若励磁系统产生的磁场在传感器测量管内呈均匀分布，且磁场方向沿X轴方向，由式（8）可知WZ∝jY，则通过求解虚电流密度分布即可得到传感器权重函数。以普通的长筒电磁流量计为例，利用ANSYS有限方法求解权重函数的过程和结果如下。

    ①有限元求解二维模型的建立

    模型建立步骤包括设置求解区域、定义求解单元类型、材料特性和初始参数设置等。在此，将传感器测量管半径设置为50cm、点电极直径设置为5mm、电单元类型选择PLANE230，电极选择不锈钢材料、电阻率设置为1.75×10-8Ω·m、液体电阻率设置为1.8×10-3Ω·m。

    ②有限元求解

    有限元求解包括网格划分、施加边界条件和载荷、求解器设置等。采用自由网格划分网格，得到传感器求解域的网格模型如图2所示。

图2 传感器网格模型

    求解类型选择稳态分析，求解器类型选择波前解算器。边界条件设置如下：测量管为绝缘管壁，因而管壁处有∂G/∂n=0，无电荷泄漏；电极为导电体，其表面电位为等势电位。

    ③结果数据输出及显示

    对求解得到的虚电流密度数进行数据分析处理，*终得到传感器权重函数。采用有限元计算得到的长筒式电磁流量传感器的权重函数数据分布和通过解析法得到的权重函数数据分布分别。    

  采用有限元数值计算得到的长筒式电磁流量计权重函数与采用解析法得到的权重函数数据非常接近，两者之间的数据偏差与网格密度和边界条件设置等因素有关。上述分析结果也证明了采用有限元计算电磁流量计权重函数是高效、可行的研究方法，它为优化非满管电磁流量传感器结构提供了理论依据。

    2 非满管电磁流量传感器

    2.1 非满管电磁流量传感器结构

    本文设计了一种具有长弧形电极的非满管电磁流量传感器。

    非满管电磁流量传感器测量管壁上设有一对长弧形电极，作为流速和液位信号的测量电极；传感器底部设有一对激励电极，用于施加液位测量的电压激励信号。传感器对非满管内的液体流速和液位实行分时测量，得到非满管内流体的流速和液位高度值。根据测得的流速和液位值，可计算得到非满管内流体的体积流量，从而实现对非满管流量的测量功能。

    2.2 权重函数有限元计算

    权重函数反映了管内液体介质单元在磁场下运动时产生的感应电势对电磁流量传感器流量信号贡献能力的大小，即电磁流量传感器测量信号是所有介质单元按不同权重数对传感器贡献的总和。当非满管内液体介质区域发生变化，即管内充满度变化时，传感器权重函数将随之改变。

    平均权重函数的计算公式为：

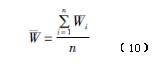
    根据所定义的平均权重函数计算公式，求得长弧形电极非满管电磁流量传感器在不同充满度下的平均权重函数变化如图4所示。

   为研究长弧形电极非满管电磁流量传感器流速测量特性，需要计算在不同液体充满度条件下的传感器权重函数。在此，取充满度α在0.1～1.0之间的10个样本，在均匀磁场的条件下，利用有限元方法对长弧形电极非满管电磁流量传感器权重函数进行计算，在不同充满度下，所得到的非管电磁流量传感器权重函数分布如图5所示。

  本文采用有限元数值分析方法，对长弧形电极非满管电磁流量计权重函数进行分析计算，得出了不同充满度下非满管传感器权重函数值。计算结果表明，非满管电磁流量传感器权重函数受管内液位变化的影响。权重函数随液位变化使得传感器在进行非满管流体流速测量时，传感器的输出信号不仅和流速有关，而且还和液位有关。因此，非满管传感器流速测量的标定系数将与液位呈复杂函数关系，不再为常值。这一结论为非满管电磁流量传感器的结构设计及传感器标定提供了理论指导。